受験生の皆様お疲れ様です。大志ゼミの土肥と申します。
3月の大きなイベントの一つといえば、県立高等学校入学試験ですね。
私も毎年の恒例行事として、試験後に問題の解答を拝見しております。今年の国語の問題は、私と同じ名前の登場人物がいてドッキリしました。たとえ小説の中でも、自分との共通点が見つかると親近感がわきますね。
さて、今回は、今年度の数学で私が気になったポイントをまとめてみました。将来受験される方々も、すでに体験済みの方々も共感していただけると嬉しいです。以下、3問ご紹介いたします。
- 大問3「規則性の問題」

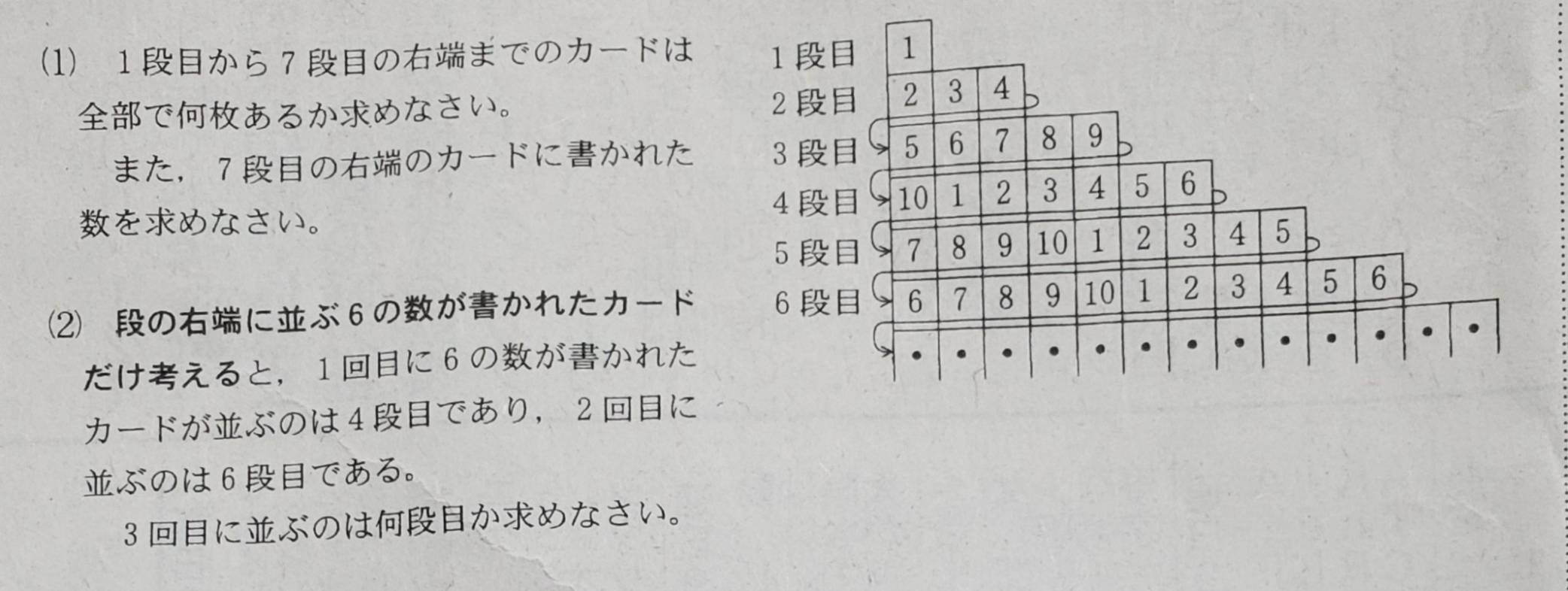
1段目は1枚、2段目は3枚、3段目は5枚、・・・、n段目は(2nー1)枚
とカードを並べた場合、その段までの合計枚数(奇数の総和)は「nの2乗」になることに気が付けば解けましたね。問題文では、あえて「〇段目の一番右のカード」に視点が向くような表現になっており、
「4段目右端のカードは6」、「5段目右端のカードは5」、「6段目右端のカードは6」と、2乗の法則が図だけでは見えづらくなっているところにひねりを感じました。
(1)で一度枚数を数えさせる追加問題がヒントになっているところに出題の意図が現れて、面白い問題でした。
- 大問4「ヒストグラム、連立方程式の問題」
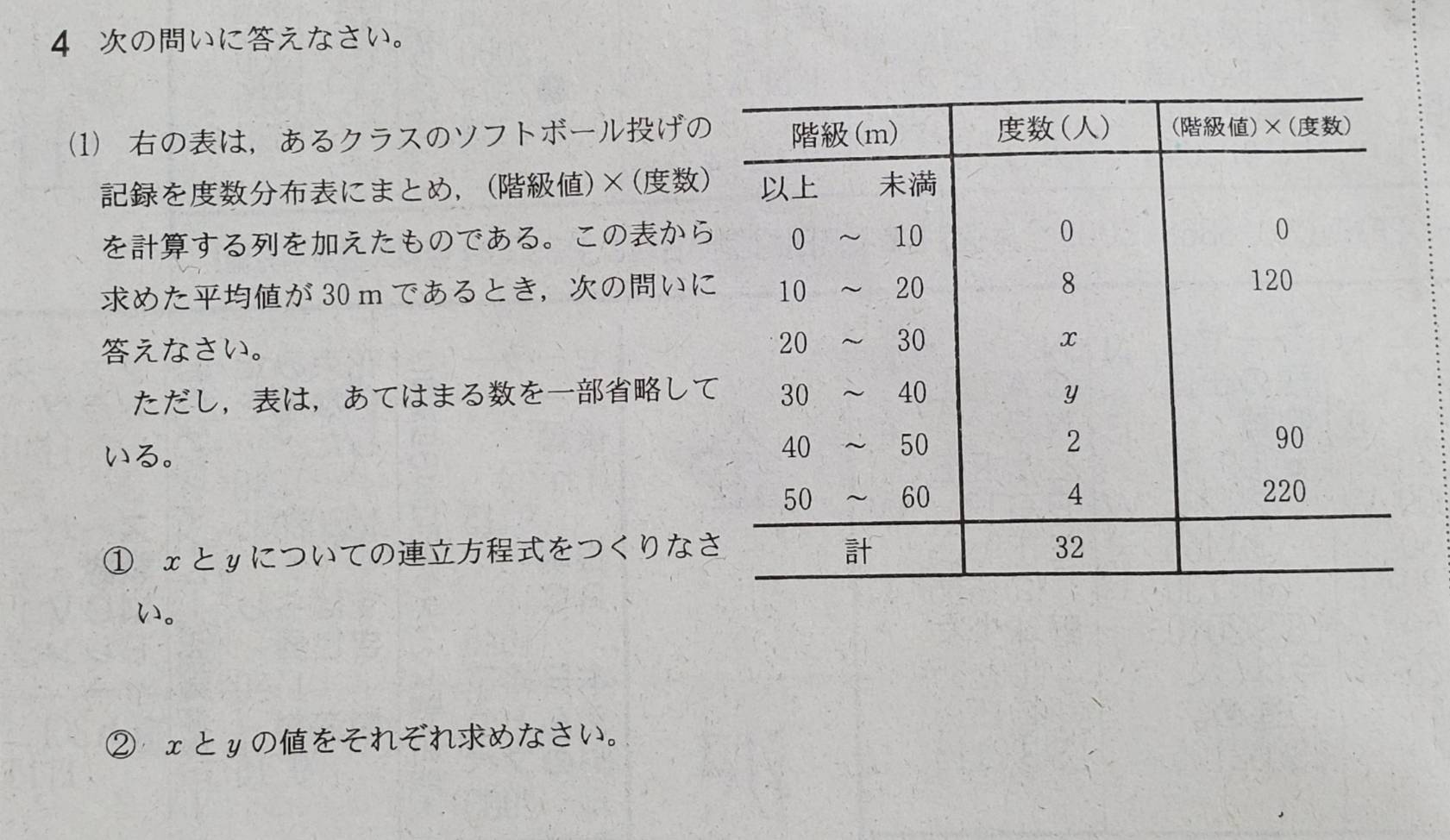
2018年度まで毎年出題されていた「連立方程式」の問題が、思わぬタイミングで出てきました。教科書にも出てくる「階級値」、「平均値」の意味を知っていればできない問題ではありません。
題のように連立方程式をたてられるということは、その問題の本質を十分に理解し、考えをアウトプットする力が身についている証拠です。ぜひ、解けるようになりたいですね。
また、公開されている解答と異なりますが、
0+8+x+y+2+4=32
0+120+25x+35y+90+220=30×32
という連立方程式は正解になるかぜひ伺いたいです。「方程式をたてる」という意味で正解ならば、計算ミスによるリスク分散のためにおすすめしたいです。
- 大問6「グラフ活用」の問題

近年の出題傾向を見ると、複数の直線または放物線のグラフを組み合わせて出題する形式が定番になっていますね。特に今回は、いつ・だれが・どこにいるか時系列を追ってみられる活用問題にも思えます。
・速度が等しい ⇒ グラフの傾きが平行または上下反転した傾き
・時間、距離を求めたいときはx座標、y座標の差を求める 等
グラフを図形問題として解けるという裏技も存在します。案外、解法の選択肢が広い問題ですので、解き方に個性がみえて面白いと思います。
以上になりますがいかがでしたか?
全体的に、普段のドリルとは異なる出題形式ですので、こういった表現に慣れるという意味で繰り返し練習していきたいですね。

















