私(安田)は、ふだん高校生に数学や物理を主に教えています。
気になるのは数学の図形問題の苦手さ加減が”半端”ないと感じています。
特に、ベクトルや空間図形の体積を求める問題では
図形の形状が思い浮かばないと、手の施しようがありません。
平面図形の場合、よく知られているピタゴラスや円がらみの定理や
チェバ・メネラウスの定理を用いるとその多くは何とかなります。
しかし、空間図形となると、図形が見えていないとお手上げになります。
さらに、見えている部分はいいとして、
見えないところの想像ができないと、何をどう用いていいのか
さっぱりの状態となります。
例えば、平面を回転させたりした図を上下左右前後から見える形を
想像することは、回転体ですから何とかなります。
しかし、立体をある軸を中心に回転してその体積をもとめたり、
異なる立体同士を交差させて、その交わったところの体積を求めようとすると
その生徒が持っている、空間の認識能力というものが多いに重要となります。
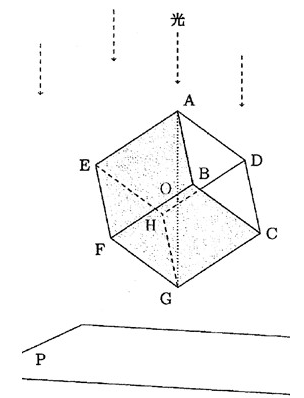
一つ例を出しましょう。
立方体があります。それを、対角線を垂直に立て上から光を当てたとき、
下面ではどのような図になり、その面積を問うのが問題でした。
今年度の慶応義塾大学環境情報学部で出題されています。
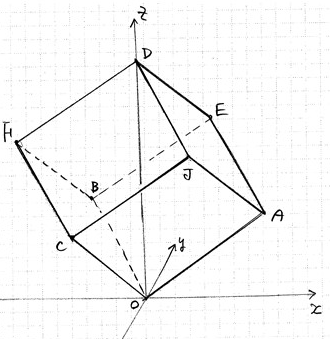
また、同じような図形が2018年度の東京理科大学理学部でも出題されています。
こちらは問題文に図は掲載されていませんが。
その問題では、上記のZ軸(OD)を中心に回転させた時の立体の体積を問うています。
皆さんはどのような空間図形を想像されますでしょうか。
透視図法や平面図・立面図を用いて
空間図形の概要を描くことができることは大事な力です。
ところで、これは生徒によく言っていますが、
入試問題では、センター試験をはじめとして、
問題文に適った図はほとんど、あらかじめ書かれていません。
数式、条件などで想像するしかないのです。
そのような時、いったん答に描かれている図を見てしまうと
せっかくの空間認識能力を鍛えるチャンスを損なうこととなります。
苦しくとも、我慢して自分なりの図を思い描いてから、答えの図をみて
自分の考えで不足していた点に気付くようにし向けて行くといいと思います。
★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★
今年で27年目を迎える JR富山駅前の学習塾
J型(自立型)個別指導
K型(解決型)個別指導
少人数一斉授業「わかばゼミ」
ホームページ:https://www.wakaba-kai.co.jp/
体験授業申込:https://www.wakaba-kai.co.jp/contact/entry.html
お問い合わせ:https://www.wakaba-kai.co.jp/contact/
☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆














