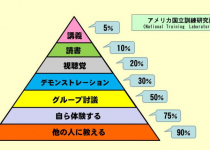
「知識と勉強ができることの関係」を考えてみます。
前回のブログで、勉強ができる人の特徴をあげました。
(https://jyukuerabi.com/detail/98/blog/4689)
勉強ができる人は、そうでない人より多くの知識を持
っていることは同意していただけると思います。
ある問題を例にして、知識がどのように使われていく
と、新しいステージに到達できるのかを考えてみよう
と思います。
小4で、「長方形の面積の公式」を学習します。
公式は、〖 長方形の面積 = たて × よこ 〗です。
では、長方形の面積を求めることができるようになっ
たら、つまり公式を覚えたら、下記の(A)のような、
1mの道を除いた部分のア~エの面積の和を求める問題
をどう考えるのでしょうか。
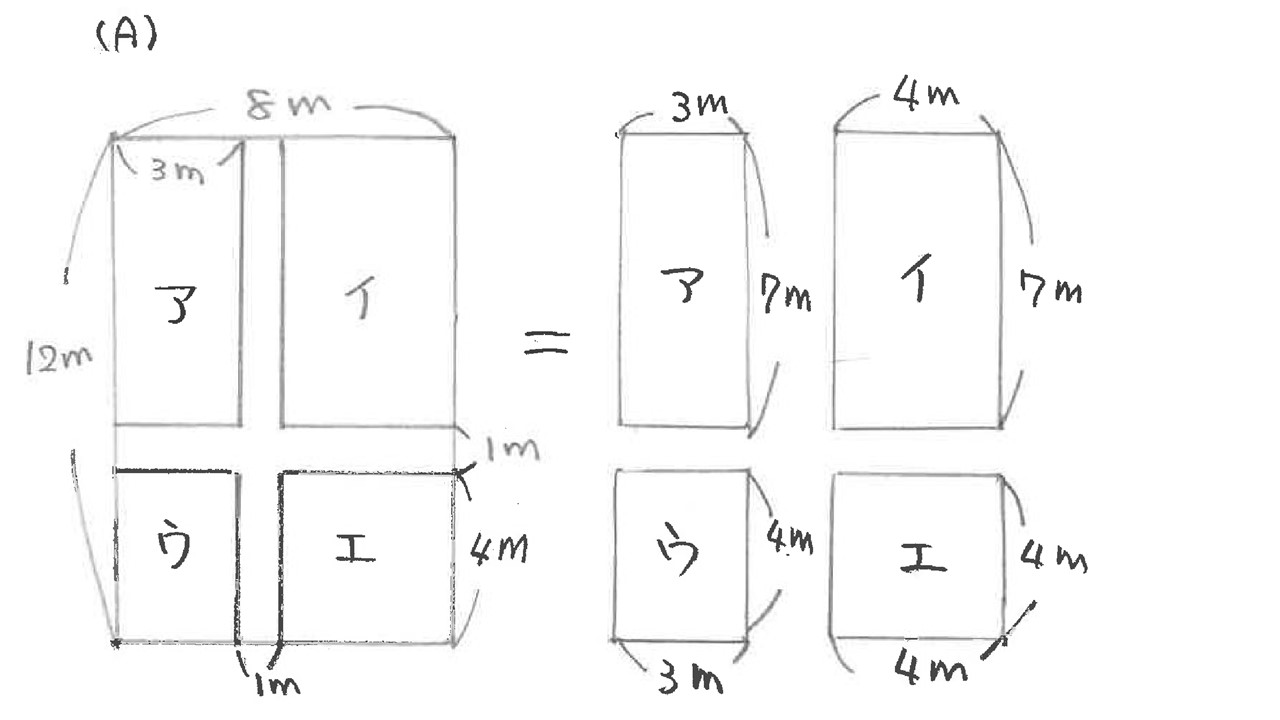
最も考え易いのは、右に示したように
求める部分を4つに分けて加えることですね。
あるいは、(B)のように全体から道の面積を引き算する
方法もあります。しかし、十字形の面積は、重なりに
注意が必要ですね。
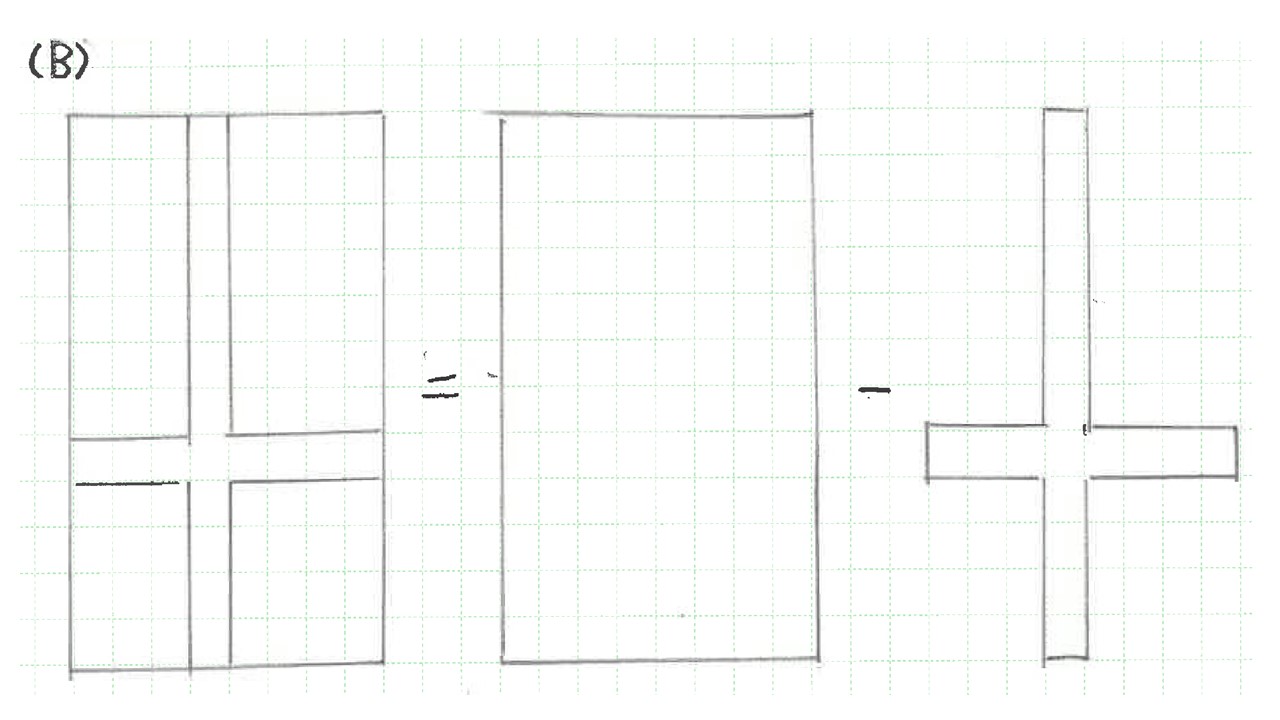
では次の(C)のような場面ではどうでしょうか。
ここでは、1mの道の場所が定まっていないため、
4つに分けたくとも、分けて求めることができません。
それでも、(B)の方法は使えそうですね。
ほかの方法はないでしょうか。
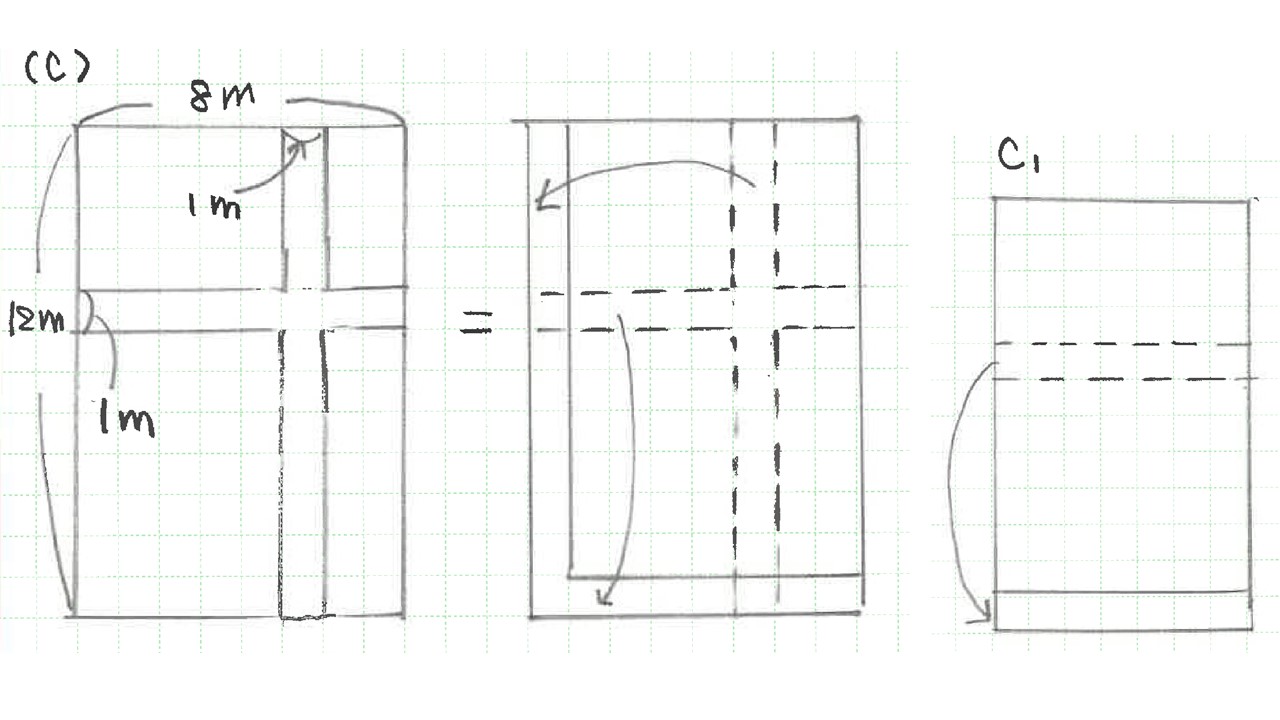
するとここで必要な知識は、C1のように道を動かして
も面積は変化しない、ということです。
そこで、(C)の様に、2つの道を動かすと、とても簡単に
求めることがわかります。
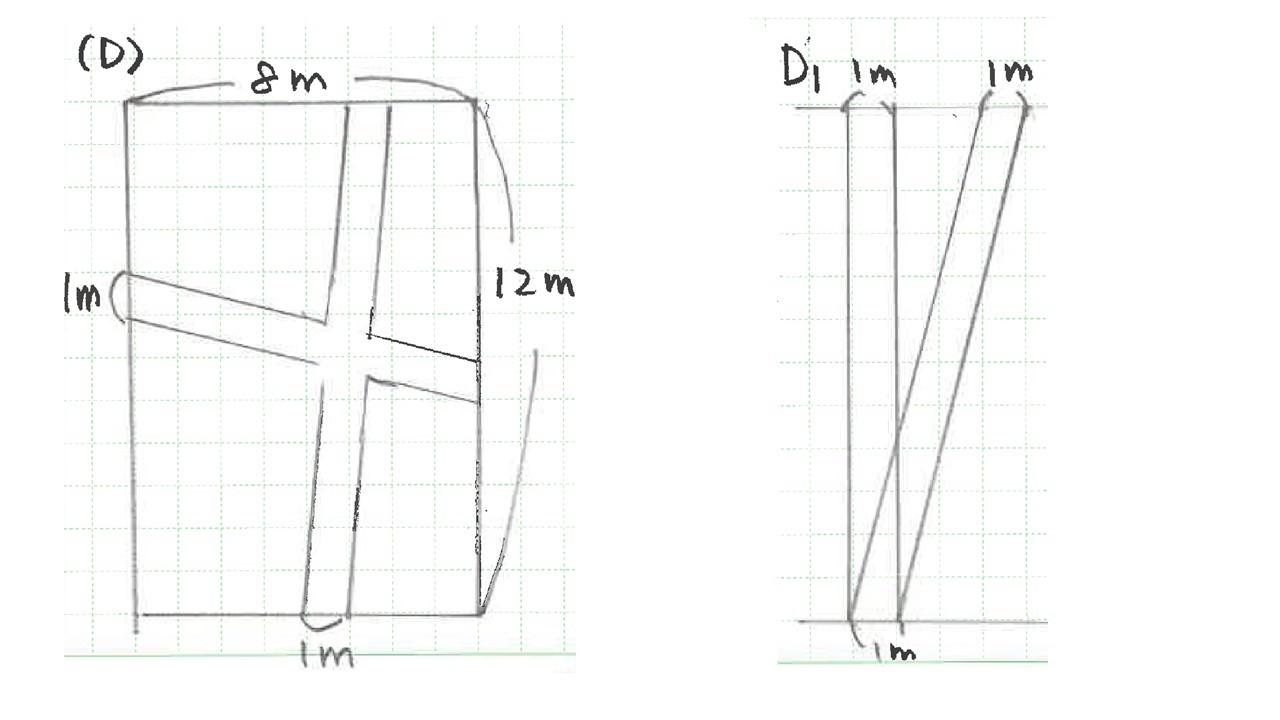
さらに、(D)の様に道が斜めだったらどうでしょうか。
この時は、D1の様に斜めであっても面積は変わらない
という知識が必要です。答えは同じですね。
「たて × よこ」という公式(知識)だけでは、道の
場所が定まっていない(C)(D)の問題は、求めること
が出来ません。
答を求めるだけなら、(B)の方法でも可能です。
しかし、それに満足せず、移動しても面積は変わらな
いという別の知識と面積の公式を結びつけることによ
って、新たな地平に到達できたということを、示して
いるのではないでしょうか。
こうして、ある知識とそれを補完する別の知識を結び
つけることによって、勉強は飛躍していくと思います。
さらに、いろいろな知識が、単なる”寄せ集め”状態に
あるのではなく、取り出しやすいように収納されている
ことも大事なことだろうと思います。
そして、このことはすべての勉強において成立している
ことと思います。
おそらく、勉強ができる人はこれら知識の整理の仕方が
ほかの人より優れているのでしょうね。

・個別指導などの、無料体験授業は随時受け付けています。
ご遠慮なく、下記サイトからお申し込み下さい。
体験授業のお問合せ
https://www.wakaba-kai.co.jp/contact/entry.html
塾へのご質問等はこちらから
https://www.wakaba-kai.co.jp/contact/
・わかば会はこんな塾 ⇒わかば会の塾紹介のまとめ
https://jyukuerabi.com/detail/98/blog/4403
★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★
今年で27年目を迎える JR富山駅前の個別指導の学習塾
各コースのご案内は下記をクリックしてください。
J型(自立型)個別指導
K型(解決型)個別指導
少人数一斉授業「わかばゼミ」
☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆★☆